Tensor Decomposition

These 2 types of methods distinguish themselves based on their answer to the following question: "Will I use the same amount of memory to store the model trained on $100$ examples than to store a model trained on $10 000$ of them ? " If yes then you are using a parametric model. If not, you are using a non-parametric model.

• Parametric:
  • The memory used to store a model trained on $100$ observations is the same as for a model trained on $10 000$ of them .
  • I.e: The number of parameters is fixed.
  • Computationally less expensive to store and predict.
  • Less variance.
  • More bias.
  • Makes more assumption on the data to fit less parameters.
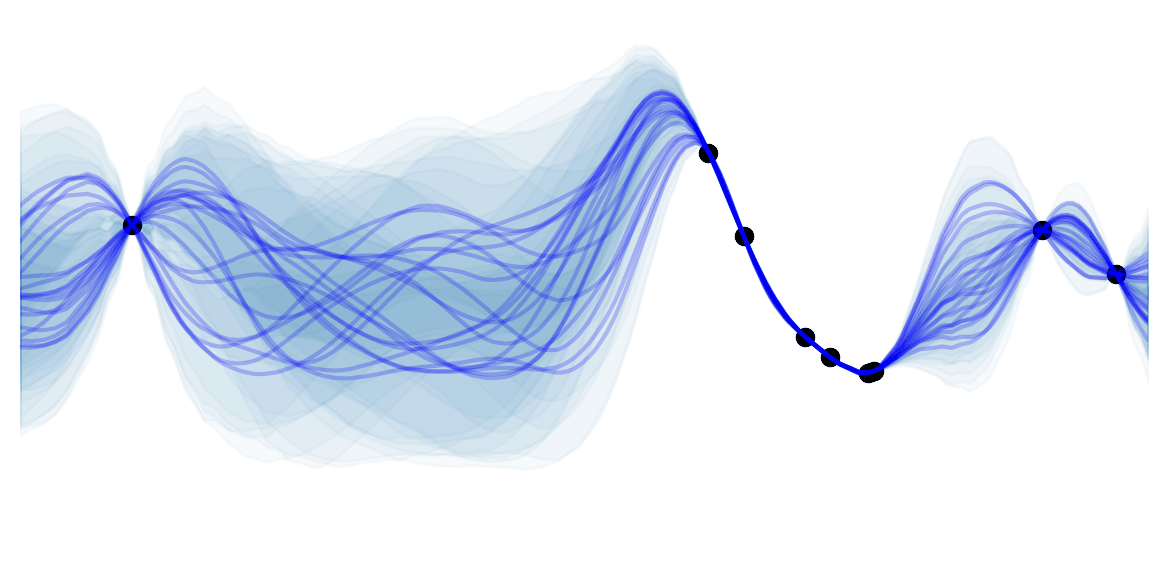
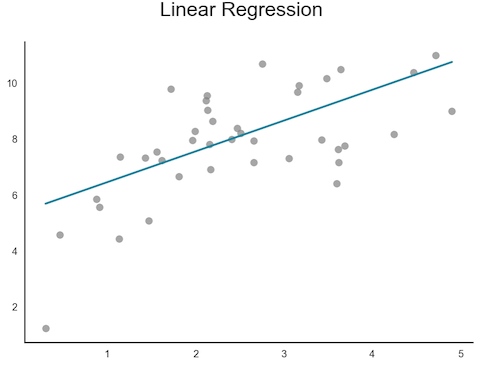
  • Example : K-Means clustering, Linear Regression, Neural Networks:

  

• Non Parametric:
  • I will use less memory to store a model trained on $100$ observation than for a model trained on $10 000$ of them .
  • I.e: The number of parameters is grows with the training set.
  • More flexible / general.
  • Makes less assumptions.
  • Less bias.
  • More variance.
  • Bad if test set is relatively different than train set.
  • Computationally more expensive as it has to store and compute over a higher number of "parameters" (unbounded).
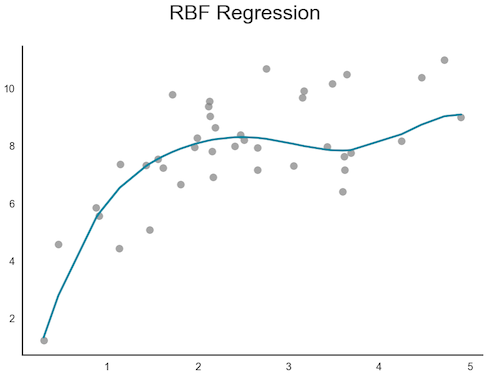
  • Example : K-Nearest Neighbors clustering, RBF Regression, Gaussian Processes:

  

Practical : Start with a parametric model. It's often worth trying a non-parametric model if: you are doing clustering, or the training data is not too big but the problem is very hard.

Side Note : Strictly speaking any non-parametric model could be seen as a infinite-parametric model. So if you want to be picky: next time you hear a colleague talking about non-parametric models, tell him it's in fact parametric. I decline any liability for the consequence on your relationship with him/her .